Miller Indices Free Download [Latest 2022]

tecimorpeecan

Jun 5, 20226 min read

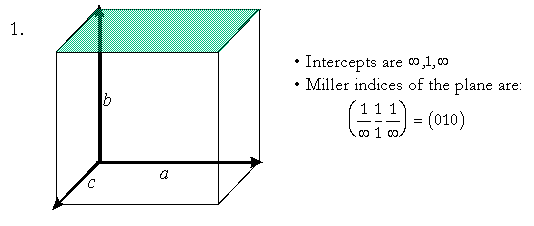
Miller Indices Crack Activation Code With Keygen Download For Windows (2022) You will learn how to define a plane using the Miller indices, the relationship between the Miller indices and the convention to use the unit vector to describe a plane. Reciprocal lattice vectors: The reciprocal lattice vectors are used to describe the plane and the reciprocal lattice factor is used to define the Miller indices. Reciprocal lattice vectors: This figure shows the definition of a plane using the Miller indices. Note that the Miller indices only specify the direction of the vector. They do not describe the magnitude of the vector and thus it will have infinite length. In this figure: .d.d. is the primitive vector .d. is the reciprocal primitive vector . is the plane in the reciprocal space. Reciprocal lattice vectors: In this figure: . is the reciprocal lattice vector. Reciprocal lattice vectors: In this figure: Note that the reciprocal lattice vectors have infinite length and thus can not be used to describe a plane. Reciprocal lattice vectors: In this figure: .d. is the reciprocal vector . is the reciprocal lattice vector . is the plane in the reciprocal space Plane from the unit vectors: You will learn how to find the plane normal vector from the unit vectors and the Miller indices. Plane from the unit vectors: In this figure: . is the plane in the original space . is the unit vectors .d.d. is the plane normal vector of the plane in the original space. Plane from the unit vectors: In this figure: .d. is the plane normal vector .d. is the plane in the original space Plane normal vector and the plane of origin: You will learn how to find the direction of the normal vector of the plane from the direction of the origin and the plane. Plane normal vector and the plane of origin: In this figure: . is the plane normal vector . is the plane in the original space . is the direction of the origin .d.d. is the direction of the plane normal vector A reciprocal lattice vector and the reciprocal lattice factor: You will learn how to find the reciprocal lattice factor for a plane from the Miller indices and the reciprocal vectors. A reciprocal lattice vector and the reciprocal lattice factor: In this figure: .d.d. is the reciprocal vector Miller Indices With License Key Interactive code for people who love calculus and maybe physics too. Supports equations and limits for numeric values. It is highly interactive. Calculates the slope of a line. Allows the user to draw a line, define the start and end points, and click on a button that calculates the slope. A: Very simple maths app for Android, useful if you are doing simple maths problems. A: I find the Math Garden App for Android to be pretty good. The mobile version of Math Garden: The Math Garden Desktop version: on the other side. So an important question is: are the smaller states willing to let the state where they live grow larger? Are they willing to accept that the economic gains of immigration are for the country as a whole, and that there is an opportunity cost to their own areas? One last thing on this. When you’re a small state, you’re not part of the national picture. It’s the other way around. You’re part of the national picture. And so you have to adjust to that. You don’t get to be a sovereign nation. You get to be a regional nation. And you have to adapt to that. You can’t get all the way up there and say, “No. This is our country.” That’s not how it works. And it’s certainly not what it was intended to be. So these are the things that I think are important to know, and they are important to know because they show you what the realities are that you’re up against. You are up against them not only by what I’ve just said, but by what the commission has said. But we don’t have to like them. We just have to take them into account and understand what they mean. And if I can say one more thing about what the commission is actually doing, and let’s just talk about what they’re doing by way of the media. They’re telling people not to be racist and not to be xenophobic, but they’re telling people to say, “If 80eaf3aba8 Miller Indices ------- This app will help you understand and remember the Miller Indices. It is basically a graphical representation of lattice plains. Please send questions or feedback to: Copyright 2019 Please note that this app is a work in progress. For better results and better looking diagrams you should use the latest version of the program. The latest version of the app was released on I don't know how long the app will be available, please do not hesitate to contact me if you have any issues with the app. Requirements ------------ 1. A recent Android emulator (tested with 2.3.3). License ------- Please consider a donation or use the app for free. If you want more info about the development please follow the development page Known issues ------------ - The app is currently missing basic support for the new Android version. Some basic features and functions work fine, but some of the images are cropped, missing or turned upside down. This is because the use of the android emulator, which is a bit more limited than the desktop version, leads to some problems. - Miller Index diagrams are not displayed correctly (they are flipped). To fix this, add the "plains.xml" file to the "assets" folder (and not in the "res" folder) Instructions ------------ - Clicking on "easy" button helps you to draw lattice planes. - You have to click on "1", "2" and "3" buttons to obtain the first, second or third Miller index, respectively. - The number next to the index tells you which lattice plane is being drawn. Features -------- - The program is designed to be a tool for learning Miller indices. - Miller Index diagrams are drawn with the Miller planes. - Miller index diagrams are drawn with the Miller planes. - Miller index diagrams are drawn with the Miller planes. - Miller index diagrams are drawn with the Miller planes. - Miller index diagrams are drawn with the Miller planes. - Miller index diagrams are What's New in the Miller Indices? Miller indices are the three angles with respect to the x,y,z axes that describe the crystal lattice. They are also used to describe the various crystal lattices (e.g. cubic, hexagonal and tetrahedral). The Miller indices are used to describe the crystal lattice, the crystal planes (e.g. c-plane of the cubic lattice, a-plane of the hexagonal lattice and b-plane of the tetrahedral lattice). The Miller indices are generally written as a vector and the direction of the vector indicates the direction of the reciprocal lattice vector, which is also called the reciprocal space vector. The Miller indices are usually expressed as a right hand vector with the unit vector component on the right hand end. Functionality: The Miller indices can be expressed with a vector or through the use of a radial vector. The basis vectors of the 3x3 reciprocal lattice can be described by the three Miller indices or the three reciprocal basis vectors. The Miller indices can also be described in terms of the reciprocal lattice factor or vector. The unit vectors are shown by circles and the radius of the circle is related to the magnitude of the reciprocal lattice vector. The Miller indices can be used in crystal structure databases for describing the crystal lattice. The Miller indices can also be used to describe the crystal lattice planes (e.g. c-plane of the cubic lattice, a-plane of the hexagonal lattice and b-plane of the tetrahedral lattice). The Miller indices can be used to describe the unit vectors of the crystal lattice planes and a spherical coordinate system can be used to describe the Miller indices of the crystal lattice. The Miller indices can be used to describe the orientation of crystal lattices. The Miller indices can be used to describe crystal symmetries. The 3-fold rotational symmetry can be described using the Miller indices. The Miller indices can be used to describe the space group symmetry of the crystal. The Miller indices can be used to describe crystal twinning. The Miller indices can also be used to describe other types of symmetry transformations. The Miller indices can be used to describe the crystallographic directions. The crystallographic directions can be described using the Miller indices. The Miller indices can be used to describe the crystallographic axes. The crystallographic axes can be described using the Miller indices. The Miller indices can be used to describe the crystal structure of a crystal. Credits: Jacob Stöhr from the University of Hamburg and Patricia Stangl from the TU Graz. Examples:   Miller index vector   In this example, the Miller indices are used to describe the crystal lattice. The basis System Requirements: System Requirements: Requires OS: Windows XP Service Pack 3 CPU: Intel Pentium 4 or AMD Athlon Memory: RAM: 1 GB Hard Drive: 60 GB available space Video: ATI Radeon X300 256 MB graphics card or NVIDIA Geforce 4 DirectX: Version 9.0c Mac OS X: Apple Mac OS X v10.5.8 or later Linux: Ubuntu 11.10 or later requires. Intel Pentium 4 or AMD AthlonRAM: 1 GBHard Drive: 60 GB

Miller Indices Free Download [Latest 2022]

Recent Posts

Comments